Tutorial 4: calculate the dipole moment of Ag55

This tutorial show how to use the comp_dipole_moment module of PyNAO including:

calculation of the dipole moment for delta-kick excitation
calculation of dipole strength function
calculation of dipole moment for Gaussian pulse excitation

First, run or load a simulation in frequency domain. The frequencies are selected based on time instances for which the dipole moment is to be calculated.

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio

from pynao import tddft_iter
from pynao.m_comp_spatial_distributions import spatial_distribution
import pynao.m_siesta_units as msu
import pynao.m_comp_dipole_moment as dipole
import pynao.m_fft as ft

Ha = msu['ha2ev']
fs = msu['fs2autime']

eps = 0.05/Ha # iterative broadening
t1 = np.linspace(0,10,100) # in fs
run_sim = False

if run_sim:
    # run tddft calculation
    td = tddft_iter(label="siesta", iter_broadening=eps, xc_code='LDA,PZ')

    w2 = dipole.comp_omegas(t1*fs)

    omegas = w2 + 1j*td.eps
    dn0, p_mat = td.comp_dens_along_Eext(omegas, Eext=np.array([1.0, 0.0, 0.0]),inter=True)
    eps = td.eps
    sio.savemat('result.mat',{'omegas':omegas,'p_mat':p_mat,'eps':eps})
else:
    w = sio.loadmat('result.mat')
    omegas, polarizability = (w['omegas'][0],w['p_mat'][0,0,:])
polarizability = -polarizability
omegas = omegas.real

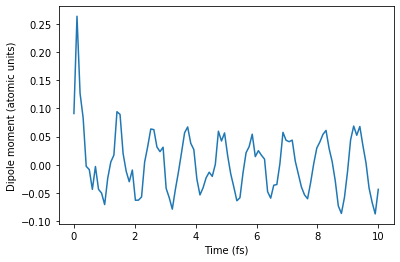
Dipole moment calculation:

dm_kick = dipole.comp_dipole_moment_kick(omegas, polarizability, eps=eps, kick_magnitude=1e-3)

plt.plot(t1, dm_kick)
plt.xlabel('Time (fs)')
plt.ylabel('Dipole moment (atomic units)')
plt.show()

/opt/conda/lib/python3.7/site-packages/numpy/core/_asarray.py:85: ComplexWarning: Casting complex values to real discards the imaginary part
  return array(a, dtype, copy=False, order=order)

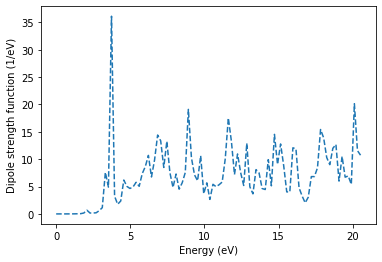
Computation of dipole strength function:

import scipy.io as sio
plt.plot(omegas*Ha,dipole.comp_dipole_strength_function(omegas, polarizability)/Ha)
plt.xlabel('Energy (eV)')
plt.ylabel('Dipole strength function (1/eV)')
plt.show()

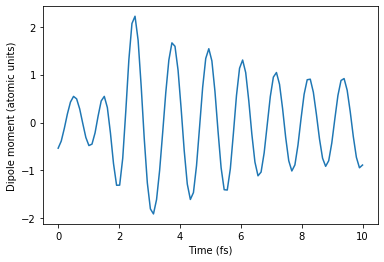
Computation of dipole moment for a Gaussian pulse

p = dipole.comp_dipole_moment_gauss(omegas, polarizability, amplitude = 1e-3, center_frequency = 3.65 / Ha,
                                    center_time = 2.303 * fs,
                                    duration = 0.8225 * fs)
plt.plot(t1,p)
plt.xlabel('Time (fs)')
plt.ylabel('Dipole moment (atomic units)')
plt.show()

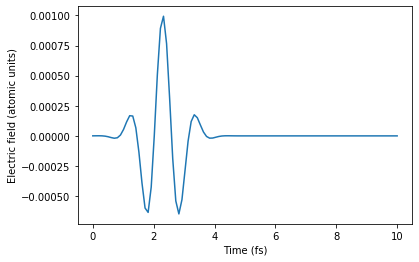
amplitude = 1e-3
center_frequency = 3.65/Ha
center_time = 2.303*fs
duration = 0.8225*fs
gp = dipole.gaussian_pulse(t1*fs, amplitude, center_frequency, center_time, duration)

plt.plot(t1, gp)
plt.xlabel('Time (fs)')
plt.ylabel('Electric field (atomic units)')
plt.show()